My husband Frank Johnson took the headshot of Fibonacci’s statue in  Pisa, Italy, in 1978. While Fibonacci, Leonardo Pisano, is known for the sequence 1, 1, 2, 3, 5, 8, 13, 21, ..., he actually did something much more important. In 1202, he introduced the concept of zero as a placeholder and the Hindu-Arabic numerals in use today to Europe. Before that, computations were done on the abacus and recorded in Roman numerals. Fibonacci also showed how to calculate using fractions and decimals; to grasp the significance, try to do long division or to calculate a salesman’s commission using Roman numerals.  Leonardo “Fibonacci” Pisano was the foremost mathematician in Europe in 1200.

Also, Fibonacci numbers are closely related the famous “golden ratio.”

Fibonacci Number information is found from the link below.

Click here for Fibonacci numbers

How the Maya Constructed the Golden Rectangle

Maya priests and Greek Pythagoreans had much in common. The Maya believed that the measuring of the square with a cord was the first action of the gods when they created the Cosmos and saw the harmony of the Cosmos in their geometry. The Pythagoreans saw numbers as the ultimate reality and found harmony in the mathematical movements of planets and stars.

Thousands of miles from Greece, the Maya used simple cords to lay the groundwork for buildings. They used a cord to form a figure with four equal sides and then squared the angles by insuring that the diagonals were equal. Each pyramid had a square base, the fundamental shape of Maya geometry and the module from which all Creation was generated.

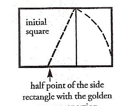
Like Pythagoras, the Maya saw harmony in the golden mean and developed a simple procedure for creating that proportion by first forming a square. The builders halved the cord to find the center of a side and stretched the cord from that center to a corner of the square as in the figure below. Then they swung the cord down to measure out the baseline for a rectangle, the famous golden rectangle.

The golden mean, held in high regard by the Pythagoreans, appears in Greek art and architecture. The golden mean, the ratio of length to width of the golden rectangle, has value (1 + √5)/2. If the width of the rectangle above is 2, then the square has side 2 and half-side 1, and the sides of the central triangle are l, 2, and √5. The distance from the arrow to the right corner is √5 and the length of the rectangle is (1 + √5).  See diagram at top of page.

The Maya described the god’s construction of a square as: “its four sections; its four cornerings; its measurings; its four stakings.” They constructed a golden rectangle by: “its doubling-over cord measurement; its stretching cord measurement; its womb sky; its womb earth; its four sides; its four corners as it is said.” (Linda Schele and Peter Mathews, The Code of Kings, Simon and Schuster, New York, 1999: 35-36.) The Maya saw the proportions of the golden rectangle in nature and believed that houses built using the golden mean are like flowers.

The golden rectangle is closely related to the Fibonacci numbers 1, 1, 2, 3, 5, 8, 13, but how this is so is beyond the scope of this short note. Mystics love the golden ratio and the Fibonacci numbers; see Dan Brown’s bestseller, The Da Vinci Code.